近期，华人策略综合讨论大厅蒋达清教授团队在传染病模型的随机微分方程应用研究方面取得系列进展。相关成果先后刊发在Journal of Mathematical Biology（《数学生物学杂志》）、Journal of Nonlinear Science（《非线性科学杂志》）、Chaos, Solitons & Fractals（《混沌、孤立子和分形》）等国际著名期刊上。该系列成果得到国家自然科学基金、山东省自然科学基金和校自主创新基金强基计划资助。

1. 随机微分方程在HIV病毒动力学模型中的应用。

艾滋病是由感染艾滋病病毒（HIV）引起的，是一种危害性极大的传染病，它已成为21世纪对人类健康威胁最大的传染病之一。蒋达清教授研究团队和加拿大约克大学Jane M. Heffernan教授合作，依据HIV病毒发病机理，引入随机扰动因素，提出一类具有B细胞免疫应答的随机时滞HIV病毒动力学模型，探讨关键参数对随机再生数大小的影响，分析不同程度的噪声对病毒动力学行为的影响，为疾病预防控制提供理论支持和决策依据。该研究成果发表在中国数学会一区期刊Journal of Mathematical Biology上，王艳老师为第一作者，张新红副教授为合作作者，Jane M. Heffernan教授为通讯作者。

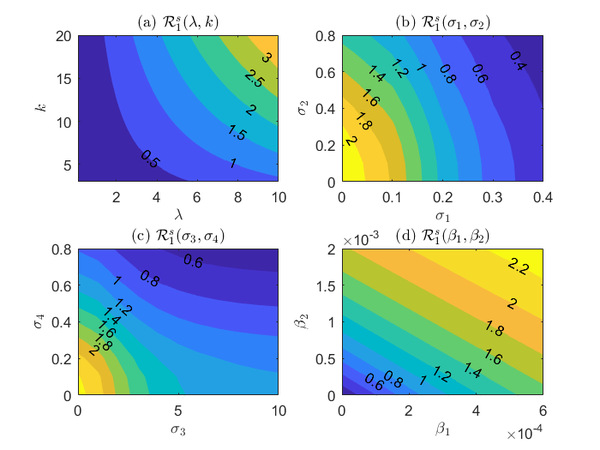
针对CTL免疫应答机制，蒋达清教授团队构建一类具有CTL免疫应答和分布时滞的随机HIV病毒动力学模型，提出模型分析的新理论，预测病毒感染的未来发展趋势。该研究成果发表在中国数学会二区期刊、中科院SCI二区期刊Journal of Nonlinear Science上，受到了审稿人的高度评价。王艳老师为第一和通讯作者，蒋达清教授为合作作者。

另外，针对被病毒感染的T细胞具有恢复阶段，构建一类具有Ornstein–Uhlenbeck过程的随机HIV病毒动力学模型，得到平稳分布的存在性和概率密度函数的精确表达式。该研究成果发表在中科院SCI一区期刊Chaos, Solitons & Fractals上，硕士研究生韩诚为第一作者，王艳老师为通讯作者，蒋达清教授为合作作者。

2. 随机微分方程在传染病动力学性质研究方面的进展。

传染病一直以来是人类的公敌，给人类社会造成了巨大的灾难和损失。特别是2020年初新冠肺炎在全球大流行，给人们的身体健康、生命安全及社会生活造成了巨大威胁和挑战。同时，生态社会不可避免地存在各种环境噪音，因此研究随机环境中传染病模型的动力学性质，对更好地预防和控制传染病的传播具有重要指导作用。蒋达清教授团队从自身优势出发，通过分析环境噪声对传染病传播过程产生的影响，构建了符合实际的具有疫苗接种的随机传染病模型，分析了疾病流行情况并预测疾病的发展趋势。相应成果发表在中国数学会二区期刊、中科院SCI二区期刊Journal of Nonlinear Science上，张新红副教授为第一和通讯作者，蒋达清教授为合作作者。

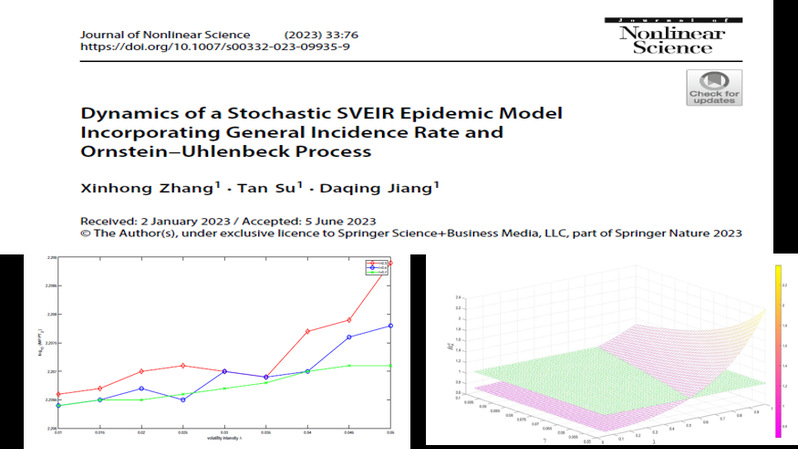
  此外，为了分析媒体报道对传染病动力学影响，通过在模型中引入媒介作用影响变量，建立了一类具有噪音干扰和媒介效应的随机传染病模型，并分析了对传染病传播过程的影响。相应成果发表在中科院SCI一区期刊Chaos, Solitons & Fractals上，博士研究生周雅欣为第一作者，蒋达清教授为通讯作者。

《Journal of Mathematical Biology》是中国数学会跨学科应用数学领域的顶级期刊，《Journal of Nonlinear Science》是中国数学会应用数学领域的二区期刊，《Chaos, Solitons & Fractals》是中科院SCI一区Top期刊。

论文链接：

https://link.springer.com/article/10.1007/s00332-023-09955-5

https://link.springer.com/article/10.1007/s00285-022-01863-8

https://www.sciencedirect.com/science/article/abs/pii/S0960077923008317

https://link.springer.com/article/10.1007/s00332-023-09935-9

https://www.sciencedirect.com/science/article/pii/S0960077923000280?via%3Dihub